Knowledge- and data-driven design of mechanical meta-materials

Overview

This is a project funded by the National Science Foundation (NSF) under the Design of Engineering Material Systems (DEMS) program and is a collaborative project between Dr. Daniel Selva and Dr. Meredith Silberstein of Cornell University. Roshan Suresh Kumar is the graduate student from SEAK Lab working on this project.

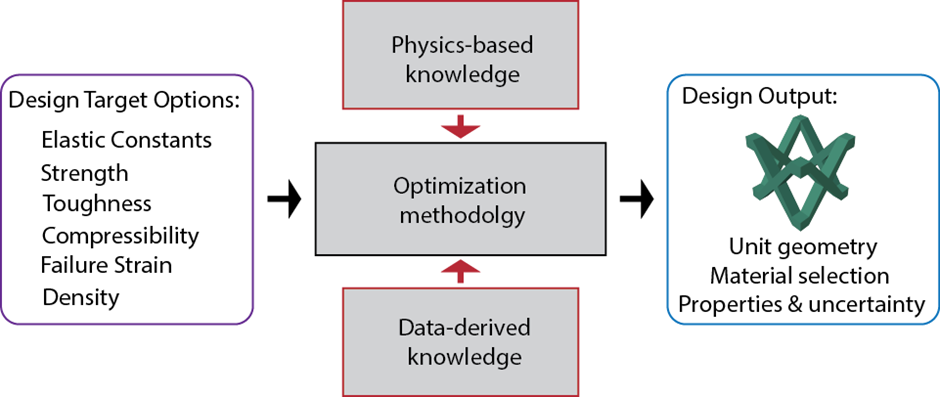
The main objective of the project is the development of a design method for 3D printable elastomeric metamaterials that leverages both expert knowledge and data (Figure 1). Metamaterials are materials that are constituted of repeated lattice unit cells. The geometry of these lattice cells directly affect the mechanical properties of the macro material. Thus, the design method will focus on the optimization of the lattice design to achieve desired mechanical properties such as high tensile strength, low volume fraction etc. Since the inverse design problem is extremely complex, involving combinatorial design decisions, non-convex, nonlinear mapping to the objectives and multiple hard-to-satisfy constraints, the employment of expert knowledge into the optimization framework will greatly improve the efficacy of the design search.

Usually, methods like topology optimization using expensive evaluation models such as FEA simulations have been utilized for these design problems. The use of surrogate models is also severely limited due to the expense of training using high fidelity models and poor performance of such models in certain regions of the design space. Expert knowledge is available in many different forms (such as physics-based models and design heuristics) and represents prior tested knowledge that can prove useful for the design problem. Moreover, the incorporation of these heuristics into the design optimization problem has not been extensively studied. In lieu of this, the specific intellectual contributions of this work are as follows:

• Guidelines about when and how it makes sense to use expert knowledge for materials design
• Strategies to effectively incorporate different types of knowledge into the design method in combination with data-driven approaches
• New materials designed through this framework
• A knowledge base for design of mechanical metamaterials

This research approach harnesses the expertise of the Selva group in engineering design, optimization, machine learning and knowledge-based systems and the expertise of the Silberstein group in polymer modelling and experimental characterization.

Significant Results

The results from the utilization of design heuristics for a multiobjective mechanical metamaterial design optimization problem were published and presented at IDETC/CIE 2021 in the paper titled “Leveraging Design Heuristics for Multi-objective Metamaterial Design Optimization.”

In the paper, the challenges in identifying and leveraging the promising design heuristics for a given design optimization problem were studied through a simple class of 2D multiobjective metamaterial design optimization problems. The design space was a 2D 3×3 node grid unit cell with 30 binary design decisions representing the presence or absence of truss members within the node grid. Unit cell repeatability in both orthogonal directions was enforced by emulating the design decisions for opposite edge members. An example design in its repeated configuration is shown in Figure 2.

The objectives were maximization of vertical stiffness (C₁₁) and minimization of unit cell volume fraction subject to three constraints. 

• The feasibility constraint dictates that designs cannot have any intersecting or overlapping members. This constraint aims to help create designs that are realizable. 
• The connectivity constraint enforces the presence of at least two connections for each used node and is related to mechanical stability. 
• The final constraint drives the design stiffness ratio C₂₂/C₁₁towards a user-defined target value. 

Four candidate design heuristics are considered for this problem that mimic the heuristics accumulated from a lessons learned database:

• The partial collapsibility heuristic is associated with shear stability and checks for the presence of diagonal members in the four rectangular sub-regions within the unit cell.
• The nodal properties heuristic helps in satisfaction of the connectivity constraint and encourages designs to have at least three connections for all used nodes and limits the number of unused nodes to 1.
• The orientation heuristic is aimed at satisfaction of the stiffness ratio constraint and directs designs to achieve a target average orientation based on the user-defined target stiffness ratio. 
• The intersection heuristic helps satisfy the feasibility constraint and limits the number of intersections between design members.

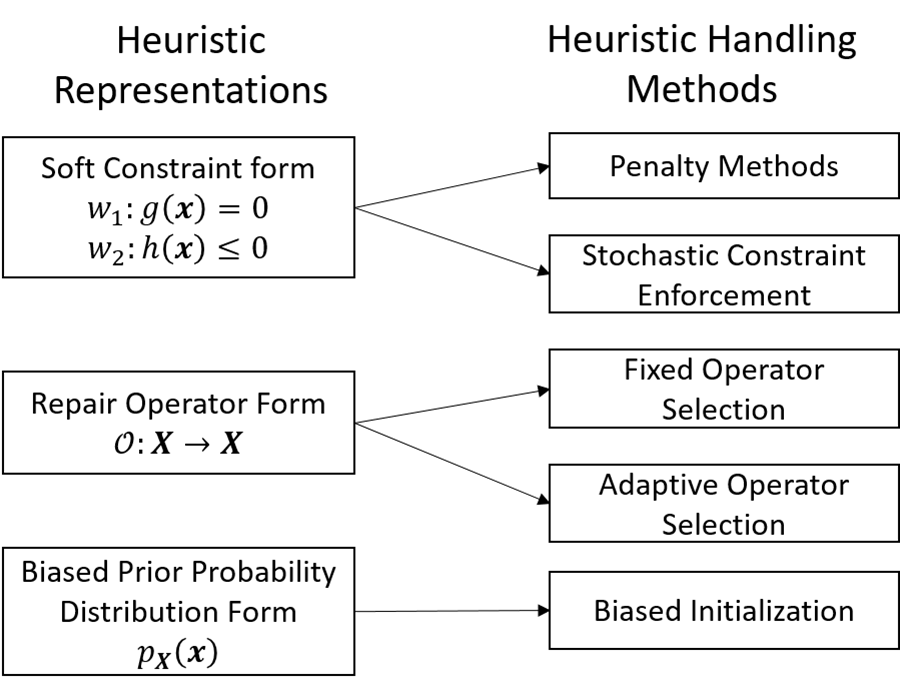
Design heuristics can be represented in different ways and the methods to enforce and leverage the heuristics in the optimization framework (called heuristic handling methods) vary based on the heuristic representations. A selection of these representations and their corresponding handling methods are shown in Figure 3.

• The soft constraint representation is a function that maps the design space to the real number space quantifying the degree of satisfaction of the heuristic (e.g., 0 indicating no satisfaction whatsoever and 1 indicating full satisfaction). The heuristic soft constraint form can be incorporated into the optimization framework using either penalty methods like Interior Penalty or stochastic constraint enforcement methods like Disjunctive Normal Form or Adaptive Constraint Handling.
• The repair operator form of a heuristic manipulates an input design to create another design that satisfies the heuristic to a greater extent. For example, the partial collapsibility repair operator adds a diagonal member at random to a design, which likely reduces the risk of collapsibility. The repair operator form of a heuristic can be leveraged either through a fixed operator selection method (which repeatedly enforces the repair operator throughout the optimization run) or through an Adaptive Operator Selection (AOS) method that maintains a pool of knowledge-dependent and knowledge-independent operators, assigns credits to operators based on their cumulative performance and probabilistically selects the operator to apply at different stages of the optimization process based on their credits.
• The biased prior probability distribution form samples a population of designs biased towards the satisfaction of a heuristic. For example, the partial collapsibility biased distribution form is a population of designs biased to have more diagonal members. The biased distribution form of a heuristic can be used as the initial population for an optimization algorithm.

To identify the promising heuristics for a particular design problem, certain metrics are introduced in the paper. These metrics quantify the ease of satisfaction of a heuristic and its targeted quantity and the correlation between the degree of satisfaction of a heuristic and being close to the true or penalized Pareto Front and the degree of satisfaction of a constraint. These metrics utilize the soft constraint forms of the heuristics and can be computed on either randomly generated designs or a combination of random designs and “good designs” obtained by running the optimization algorithm for a few iterations. These metrics include correlation coefficients (Pearson’s or Spearman’s) and interestingness measures from Association Rule Mining theory (e.g., support, confidence and lift). 

10 trials of 400 designs each (100 randomly generated and 300 from an 𝜖-MOEA run on the penalized objectives without enforcing any heuristics) were used to validate our metrics to identify promising heuristics in the metamaterial design problem. It is found using this method that orientation and intersection are the promising heuristics whereas partial collapsibility and nodal properties are not promising.  

To show that the heuristics identified as promising can indeed help accelerate the optimization, a experimental study was done consisting of four cases:

• Case 1: No heuristics enforced – control baseline. 
• Case 2: Orientation – Repair operator form handled using AOS and Intersection – Repair operator and biased distribution forms handled using AOS and biased initialization respectively
• Case 3: Orientation – Repair operator form handled using AOS
• Case 4: Partial Collapsibility and Nodal Properties – both repair operator forms handled using AOS. This is developed as a negative benchmark since these were identified as non-promising heuristics. 

For each case 30 𝜖-MOEA runs were performed with a population size of 100 and termination criteria of 3000 function evaluations. Figure 4 shows a quad chart with the feasible designs in the combined Pareto Front of all runs for all cases at different stages of the optimization process. It can be observed that Case 2, which leverages both the promising heuristics, is able to obtain feasible designs in the Pareto Front first.    

Figure 5 shows the plot of the hypervolume over the penalized objectives for all cases. Since Case 2 is the first to find feasible designs in the Pareto Front, it is also the first case to see a sharp rise in the hypervolume. Using the heuristics as in Case 2 saves 400 function evaluations compared to not using them.

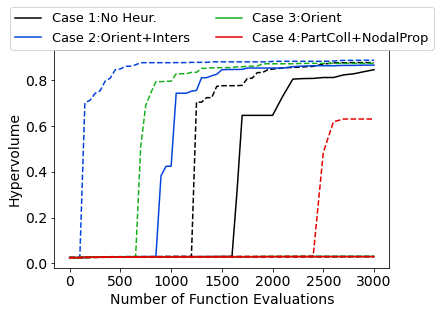
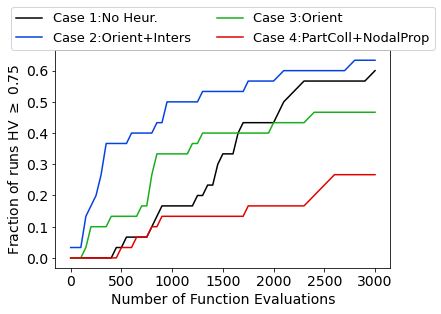
Figure 6 shows the fraction of runs for all cases to reach a threshold hypervolume of 0.75 at different stages of the optimization process. It is evident that not only does Case 2 reach the optimal design space the fastest but is also able to hold the advantage over the other cases throughout the optimization. In contrast, Case 4 which only leverages the non-promising heuristics performs worse than Case 1 where no heuristics are enforced.  

Based on these results, certain guidelines for designers to choose promising heuristics were identified and presented:

• The most useful heuristics are those that are aligned with Pareto dominance in the penalized objective space, which takes into account both objectives and constraints. In other words, a promising heuristic must be aligned with either Pareto dominance in the true objective space or with any of the constraints.
• Heuristics can be aligned with Pareto dominance only in certain regions of the design space. In this case, the heuristics must be selectively leveraged based on the current status of the optimization.
• Heuristics are typically useful mostly in the beginning of the search since they are, by definition, only directives. Therefore, over-enforcement of heuristics in the later stages of the optimization process may lead to reduced diversity. Hence, design heuristics should be eventually shut off.

A journal paper is in preparation that tests the efficacy of the metrics on two variations of an Earth Observation satellite design problem and two metamaterial design problems. Two different metrics are being developed to ascertain the promising heuristics in their soft constraint and operator forms respectively. A heuristics taxonomy is also being developed that categorizes heuristics based on their ease of satisfaction and alignment with the objectives and/or constraints. The output of the taxonomy would be a recommendation of heuristic representations and handling methods based on the perceived requirement of degree of enforcement of the heuristic.

A manuscript titled “Examining the impact of asymmetry in lattice-based mechanical metamaterials” was published in the Mechanics of Materials journal in June 2022. In this work, a generative design process is used to generate datasets of lattices with varying degrees of symmetry which are compared in terms of the presence of certain desirable properties such as negative Poisson’s ratio. Some key design features are identified which show significant correlations with the desirable properties.

Publications

Kumar, Roshan S., Srikar Srivasta, Meredith N. Silberstein, and Daniel Selva. “Leveraging Design Heuristics for Multi-Objective Metamaterial Design Optimization.” IDETC/CIE2021 (2021).

Srivatsa, Srikar, Roshan Suresh Kumar, Daniel Selva, and Meredith N. Silberstein. “Examining the impact of asymmetry in lattice-based mechanical metamaterials.” Mechanics of Materials (2022): 104386.